Then we practiced matrix multiplication by comparing matrix multiplication to the multiplication of numbers. For some students this sequence flowed really nicely. We did a problem from the homework and someone asked if we always had to bring down the matrix on the left. Cue a couple problems that follow a*b vs. b*a. Lovely counterexample of the commutative property for matrix multiplication. The next pair of problems has students multiply by the identity. For students who were paying attention they caught on to the pattern quickly and realized that this matrix was special. Students who weren't paying attention got extra practice multiplying matrices. I let them in on the 'secret' that mathematicians are lazy! They look for patterns to make their work easier and we should be like mathematicians as we work. It's a tricky balance to structure a class so that students are always looking for patterns but to make sure that they aren't just assuming there's a pattern because there always is one. That was one benefit of starting with testing the commutative property - in that case the thing to notice was the lack of a pattern! Finally we multiplied some inverses. Another benefit to the pattern finding structure is that students compared work with their group when they weren't seeing a pattern, they found mistakes faster than in a random set of practice problems. I chose my inverses very carefully which allowed students to recognize two aspects of inverses (opposite signs and switching a with d). We finished off with some homework on all the operations they've learned so far.
A few students asked during all of that rather tedious matrix multiplication practice what the point of these things was, when would anyone ever use this?? So I told them about graphic design using a matrix to represent all of the points of a figure and operations with other matrices to transform them on the screen. I could've sworn I saw a video on them using this process for the fur in Monsters Inc. at the Pixar exhibit at the Boston Museum of Science but I can't find the video online. I could, however, make up a problem set to demonstrate the process by 'animating' a triangle. This might have been my best lesson all year! It was last block before a long weekend but yet students found this lesson very approachable and got some self checking practice applying matrix operations. Bonus- I enjoy activities that blur the (non-existent) lines between algebra and geometry.
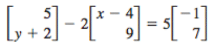 Most students finished their transformations with time to spare (in an 80 minute period) so I had another practice sheet ready to start in class and finish for homework. My colleague and I like my textbook's problems with variables and expressions as entries in matrices. Some of the entries are self checking, others make simple equations and students get some practice solving one variable equations (which, yes, my algebra 2 students do still need). However, no one on the internet has these lovely problems, including our Kuta Software. So I searched class zone (I still don't understand the structure of that site but I'm learning, kinda) and compiled all the ones they wrote on an additional equation practice sheet.
Most students finished their transformations with time to spare (in an 80 minute period) so I had another practice sheet ready to start in class and finish for homework. My colleague and I like my textbook's problems with variables and expressions as entries in matrices. Some of the entries are self checking, others make simple equations and students get some practice solving one variable equations (which, yes, my algebra 2 students do still need). However, no one on the internet has these lovely problems, including our Kuta Software. So I searched class zone (I still don't understand the structure of that site but I'm learning, kinda) and compiled all the ones they wrote on an additional equation practice sheet.Next class we'll do some other applications of matrices and row games to review the basics before heading into systems.
What else do you have for matrices? Where on the internet are these lessons hiding?


Tina, have you seen the CME Project Algebra 2 book? Lots of matrix applications.
ReplyDelete