NWMC Day 1 Recap

I attended the Northwest Mathematics Conference in Portland, OR last weekend and it was amazing. I got to hang out with so many awesome people! It was a crazy mix of tweeps and PCMI reunion and people I've never spoken to who have heard of Nix the Tricks (something that never fails to astonish me). I had so much fun that it was totally worth the stress of prepping two days of sub plans and being exhausted and (super) behind for nearly a week.

 

Friday I finally felt a normal amount of behind, so I started going through my notes and writing them up. Portland State is very generous and they are offering two grad credits to anyone who attended all three days of the conference and writes about it. There were some specific prompts to write to and I learned that my writing voice for papers is different from my blogging voice. At least it feels different. NWMC was great but not so life changing that I sound different, apparently I just write differently when typing into Word than when I compose in Blogger.

On Thursday I attended two workshops:

What makes algebra hard to learn?

Steve Rhine

This session was full of resources and links to even more resources! I look forward to thoroughly exploring the AlgebraicThinking.org website, especially their database of problems used in research. Upon return to my classroom I was pleased to discover some of the apps loaded on our school iPads are from Steve Rhine. Hearing him discuss the intentionality behind these programs makes me much more likely to use them with my students. One in particular is Point Plotter. I never would have understood the goal of this app if I just tried it – a common misconception students hold is that there are a limited number of points between two points on a line (ex: only lattice points count) – this app pushes students to find as many points as they can between two points. This addresses a misconception while simultaneously encouraging students to use the equation of the line and/or definition of slope to calculate points.

I am teaching Algebra 1 for the first time in five years and it’s been an eye (re)opening experience. I had forgotten how challenging it is to explain the basics; I wish I’d attended this session (as well as many others) during the summer so I wouldn’t have made some of the mistakes I already have with my students. Luckily it is still early in the year so I have time to address their misconceptions. One of those is the difference between an expression and an equation. As a mathematically proficient adult, it is quite obvious to me that equations and expressions are very different objects, but when I asked my students about it this week they struggled to differentiate between the two. We have all seen the mistakes where students try to ‘solve’ an expression using inverse operations – Steve Rhine shared that this can be due to students feeling “lack of closure” when their answer is an expression rather than a number as it has been for the rest of their mathematical experience.

Another place where students struggle is in understanding variables. The idea that a variable changes with different contexts but is constant within a context isn’t one I’d wrestled with, let alone helped students wrestle with. The x in problem three has no relation to the x in problem four, however, if problem five is 4x + 4 = 5x students must realize that the two x’s in that equation are the same. As a group we decided that a variable is an unknown quantity because that definition encompasses x=5 as well as x=y+3. Steve emphasized the importance of a variable representing a quantity and not an object. H can represent the height of Harry, but H doesn’t equal Harry. Instead we should refer to variables as containers. It worked out nicely that I had started equations with this pennies lesson because now I can refer to variables as cups of pennies – a mystery quantity.

Our final topic of the morning was graphing. Students struggle to understand the difference between discrete and continuous graphs. One suggestion was to ask students who connect discrete data points what the midpoint represents. For example, if they connect Sally’s height to Ted’s height, is the midpoint meaningful on that graph? Lastly, lines having constant slope is a big idea, but one that students don’t often wrestle with. If we only give students tables where the patterns jump out at them (ex: x values always increase by one) then they don’t get the opportunity to engage with the concept. We need to make sure to give students that challenge them to think and that bring out misconceptions so we can address them!

Fostering Algebraic Thinking and the CC Math Practices

Irving Lubliner

I thought the last session was full of resources, and then I got to this one – we received a bound notebook of activities! I have yet to go through the entire thing and I can’t wait to have a chance to do so. Irving Lubliner mixed teaching practices with content throughout the workshop. He made his teaching moves explicit so we could reflect on those as much as the activities. When someone gives a wrong answer he finds the question that their response correctly answers, in other words, he finds something right about their solution. We practiced for a few responses and it was a fun challenge that reminded me of My Favorite No, an activity I’ve used weekly. It would be great to infuse that spirit throughout the course. He used tickets as rewards for participation and great ideas. I am generally hesitant to give students extrinsic rewards but my school is using the PBIS model so I need to consider it. I appreciate that he rewarded bravery rather than only correct answers.

Just like my morning session, we spent time talking about expressions vs. equations. My notes say *Spend time on this!* so I had better do just that. One example in this session was about language precision – you can’t double an equation, you double each expression. When evaluating expressions he gave a great tip for getting students to remember to use the order of operations – look at the expression in chunks. This process will help students think about terms which is helpful for expressions with variables as well. Underline the expression until you see a + or -, then write “later.” Repeat until you reach the end. 200*2 + (3+4)*5 – 3*6. Next evaluate each term (in whatever order makes you happy). Then rewrite each subtraction as adding the opposite. Finally, evaluate the expression (in whatever order makes you happy). This method pushes students to think about the structure of the expression, and also allows them to use their number sense – if the expression has 15 and -15 use those opposites instead of going from left to right.

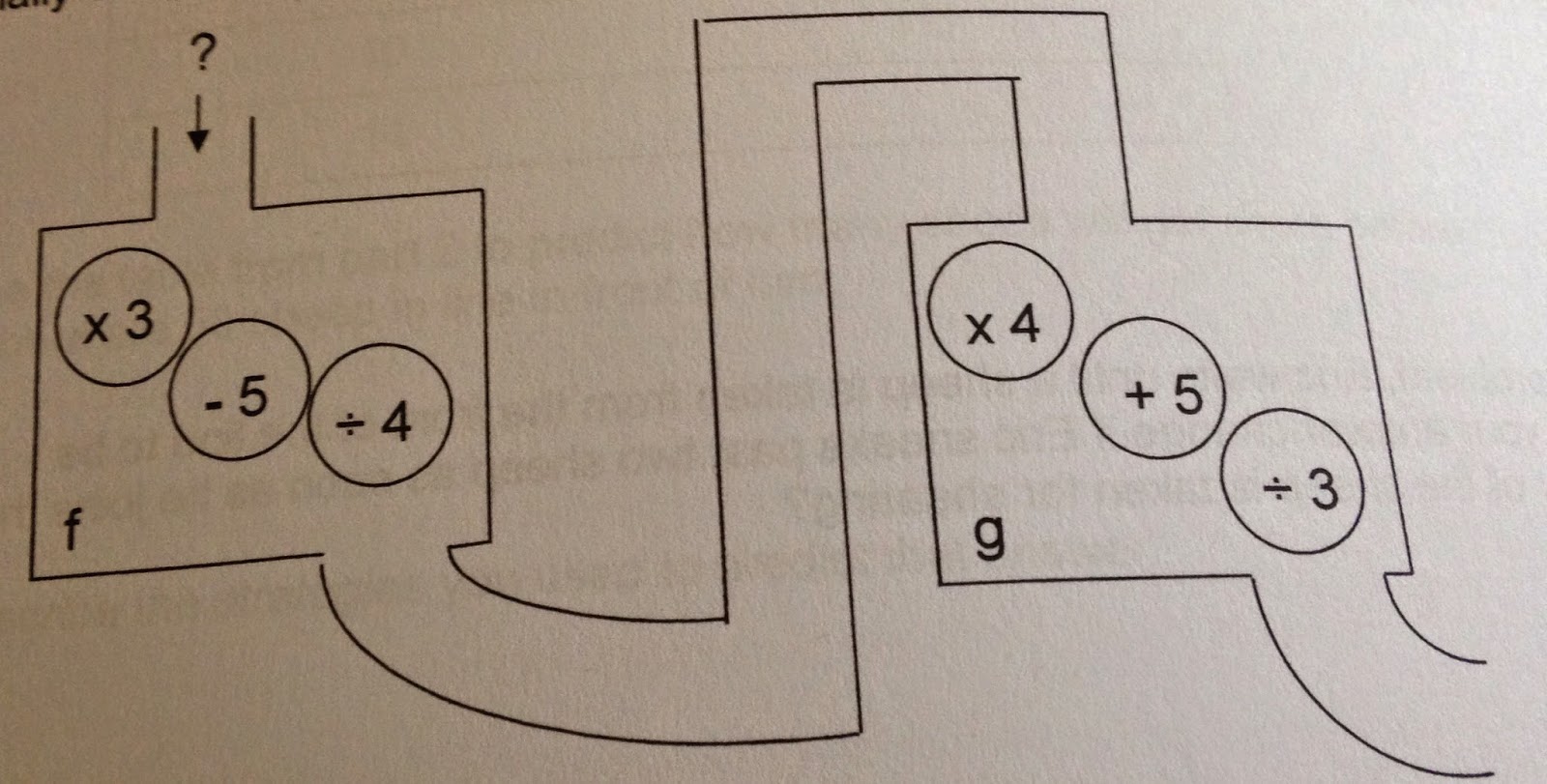
We played with a great model for solving equations. I’ve never seen the utility of a function machine model until this one: 

 

Earlier this year I tried to use a representation where we evaluated at a specific value of x to show the ‘forward’ steps, then worked back up to determine the ‘backward’ steps. This diagram is much more intuitive and shows the ‘socks and shoes principle’ clearly. During the session he showed an example with 7 or 8 steps, I wish that example had made it into the book – it made a very complicated equation seem easy. I will have to search for or recreate it since my students still need more practice solving equations.

Update 10/20/2014: The internet is awesome. Someone from NWMC saw this post and sent it to Irv and he responded with the image I was wishing for!