To start, I asked students (in groups of 3) to sort the cards based on any characteristics they wanted and told them to be prepared to share. I did not include the general formula cards yet (actually I never did- I thought I would, but plans changed!). Most students sorted into three categories - graphs, descriptions, equations - first, then started matching the corresponding graphs and descriptions (including equations when they saw a vertical parabola) or creating subgroups of the original 3 categories. After having each group share a sorting method, I asked everyone to match graph, description and equation. We quickly ran out of time but students had started learning the vocabulary (major/minor axis, vertex, center) and at least one student was hooked - I heard him say "there's an equation for a circle?!" as I walked past. Students would later refer to the cards as a game, (a word I never used), so this student wasn't the only one engaged in the lesson.
The second day students spent the entire class matching graph, description and equation. I didn't tell them anything or have them focus on one type at a time. 90 minute blocks means plenty of time for them to dive in and figure things out on their own! They struggled to find ways to match the equation. Since this happened to be Day of Silence I made a list of options to show each group as they called me over in frustration (this was an awesome day to not be talking as I wanted them to struggle with the problem and look for patterns, but once they reached unproductive struggle I was happy to give them a push in the right direction).
- Find points on the graph and check them in the equations
- make a table from the equation
- rewrite the equation so it says y= and graph it in the calculator
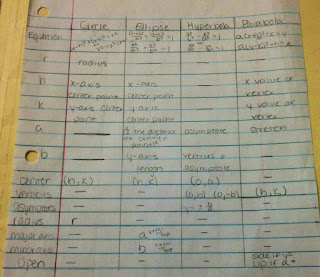
Most groups went to the calculator and got some good practice with algebraic manipulation. Another note I used over and over was "you can't distribute a square root." By the end of 80 minutes most groups had a good chunk of their cards sorted (without any instruction on the equations whatsoever!). Part of my instructions at the beginning of class said "take notes on patterns and generalizations" but I realized that students had their desks covered with cards and hadn't taken out paper. With 10 minutes remaining in class I had everyone stop and make some notes with the reminder "the cards will be shuffled before you leave and next class is two days from now so you won't remember what you figured out!" Apparently my warning was insufficiently dire because they didn't have useful notes next class. With this in mind, I would switch up the order slightly and do the dichotomous tree activity first (below), then have students sort while building their key so there was a reason and a format for their notes.
The third class I started by handing every student a creature as they entered class. The dichotomous tree (link to original pdf) was on the board and they used it to identify their creature. I used creatures 1. because they were cute! 2. because no one started out knowing their creature's name so the tree was necessary.
 |
| sample creatures, can you name them? |
 |
| I know, dichotomy means 2 and I have one that splits into 3. One student coined the term di-trichotomous tree |
 |
| Yes, that is arabic. No, I don't have any idea what it says, I had to trust her! |
From here we did some basic practice (given equation - graph and describe, given graph- write equation and describe) and then it was time for the Photo Project. (up next)
No comments:
Post a Comment