Before class I was solving this problem:
I got this problem from the website that goes along with the textbook (this matters because I'm sharing it, but it's also important to recognize that I didn't write the problem). My first step, as it is with most trig proofs, was to re-write the entire problem in terms of sine and cosine. This didn't yield any obvious simplifications, so I wondered if it was actually true. I didn't want to wrestle with the thing if it ended up being false, so I checked a couple values off to the side. For both π/4 and π/3 the equation was true, so I went back to proving it. Looking at the equation more carefully I saw that I could do the following:
This is no easy problem, for a multitude of reasons, but I could have pretended it was an easy problem, skipped showing half the steps and posted a slick, neat solution when I projected my answers. I wish I could tell you that I planned the conversation I had with my students today carefully, that leaving my scratch work had more to do with showing them my thinking than it did with my laziness, but neither of those would be true. I sure did seize the opportunity once I saw it though.
In class no one had completely solved this question so they wanted to discuss it. Looking at my solution they couldn't figure out how I had gone from all the sines and cosines to the first step you see above. This is where I walked them through exactly what I explained above. I told them how I got stuck, how I wanted to check before doing a lot of work, how I had an "aha!" moment that required going back to the beginning. I acknowledged that I had to make the problem look more complicated before it simplified. I pointed out the difference of squares, and reassured them I don't expect them to recognize that structure, yet. I explained the math practices and how recognizing structure is one of them. I talked a lot more than I usually do, but at least one of the students saw something and said "Look how excited she is about this!" To which I responded, "yes!" Thinking back about why this moment was so exciting has me realizing it's because this problem is 'real math' - this is what math looks like when mathematicians are working.
I did have a student ask "when would we ever use this?" which is a huge red flag for me; it means the math seems overwhelming and kids want an out. I explained that a) people really do use this so I want to prepare you for the possibility that you'll go into a mathematical field and b) we need a context to practice logic, reasoning and algebraic manipulation - today that context is trigonometry. They all laughed when a student said "so you just rummaged around in all of mathematics and pulled trig out of the hat?" and the original questioner seemed satisfied.
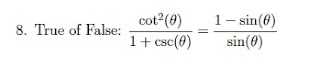

The crazy acronym is the first letters of each word up to the first vowel: NaBloPoMo
ReplyDelete